A relationship between the Collatz conjecture and the Fibonacci numbers

Introduction

In a surprising mathematical discovery, a new connection has been found between the famous Collatz conjecture and the well-known Fibonacci sequence. This relationship emerges through an infinite binary tree structure that encodes the behavior of the Collatz map in the 2-adic integers.

The Collatz Conjecture and 2-adic Integers

The Collatz conjecture concerns the behavior of the map:

$$C(n) = \begin{cases} \frac{n}{2} & \text{if } n \equiv 0 \pmod{2} \ \frac{3n+1}{2} & \text{if } n \equiv 1 \pmod{2} \end{cases}$$

It states that for any positive integer $n$, repeated application of this map will eventually reach 1. The conjecture has resisted proof for decades despite its simple formulation.

A powerful tool in studying the Collatz conjecture is the conjugacy map $\phi$, which maps 2-adic integers to other 2-adic integers such that the Collatz iteration corresponds to a simple shift operation. The inverse of this map, $\phi^{-1}$, encodes the parity (odd/even) of each iteration step as a 2-adic integer.

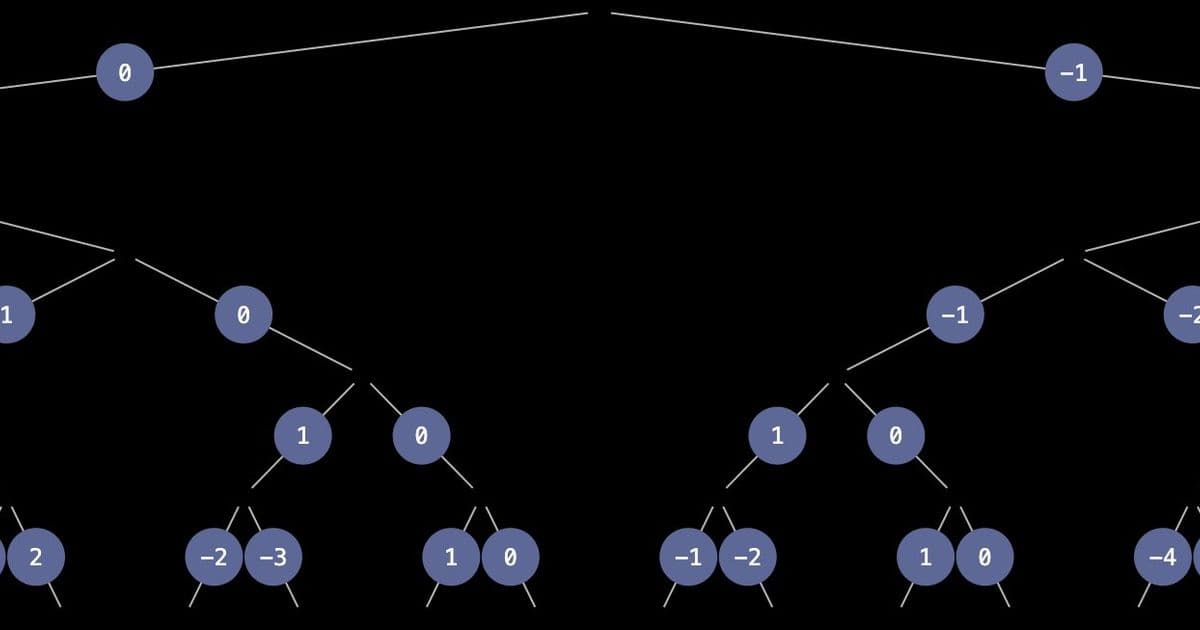
The Binary Tree Structure

The key insight is that $\phi^{-1}$ can be represented as an infinite binary tree with integer edge labels. This tree, which we'll call $R$, has the following properties:

• Each node has two children (left and right)
• Edges are labeled with integers
• The label $R(x_0, x_1, ..., x_k)$ represents the edge reached by following the path $(x_0, x_1, ..., x_k)$ through the tree
• Labels are defined recursively by: $$R(x_0, ..., x_{k+1}) = R(x_1, ..., x_{k+1}) - x_0 \cdot R(x_0, ..., x_k)$$ with initial condition $R(x_0) = -x_0$

Connection to Fibonacci Numbers

The tree $R$ contains the signed Fibonacci numbers in a remarkable way. If we follow the alternating path "right, left, right, left..." starting from the root, we obtain:

$$R(1) = -1, \quad R(1,0) = 1, \quad R(1,0,1) = -2, \quad R(1,0,1,0) = 3, ...$$

These values match the signed Fibonacci sequence $(-1, 1, -2, 3, -5, 8, ...)$.

The 2-adic Representation

For any infinite sequence $(x_k)$ of 0s and 1s, there exists a unique 2-adic integer $n$ whose Collatz iteration produces exactly that parity sequence. This value is given by:

$$n = \sum_{i=0}^{\infty} 2^i \cdot R(x_0, ..., x_i)$$

In particular, if we take the alternating sequence $(1, 0, 1, 0, ...)$, we get:

$$n = \sum_{i=0}^{\infty} 2^i \cdot F_i$$

where $F_i$ are the signed Fibonacci numbers. This sum equals 1, providing a new perspective on the well-known identity:

$$1 = \sum_{i=0}^{\infty} 2^i \cdot F_i$$

Properties of the Tree

The tree $R$ exhibits several interesting properties:

1. Self-similarity: $R(0, x_0, ..., x_k) = R(x_0, ..., x_k)$ - leading zeros can be omitted
2. Recursive structure: $R(x_0, ..., x_k) = R(x_0, ..., 0) - x_k$
3. Symmetry: $R(1, x_0, ..., x_k) = (-1)^k + \sum_{i=0}^k (-1)^{k+i} \cdot R(x_0, ..., x_i)$

These properties allow us to index the tree using non-negative integers. For $n \in \mathbb{N}0$ with binary expansion $n = \sum{i=0}^k x_i \cdot 2^i$, we define:

$$r(n) = R(x_k, ..., x_0)$$

The sequence $r(0), r(1), r(2), ...$ begins: $0, -1, 1, 0, -1, -2, 1, 0, ...$

Implications and Future Work

This discovery provides a new framework for studying the Collatz conjecture through number-theoretic methods. The connection to Fibonacci numbers suggests potential approaches using techniques from the theory of linear recurrences and Diophantine equations.

Future research directions include:

• Exploring other sequences that appear in the tree $R$
• Investigating the distribution of values in the tree
• Studying the relationship between the tree structure and the dynamics of the Collatz map
• Extending these ideas to other similar dynamical systems

Conclusion

The unexpected appearance of Fibonacci numbers in the structure of the Collatz conjecture provides a fascinating example of how seemingly unrelated areas of mathematics can be deeply connected. This discovery opens up new avenues for research and may eventually contribute to resolving one of mathematics' most famous open problems.

For more information or to discuss these findings, the author can be reached at [email protected] or on Mastodon at @[email protected].