The Subtle Bias in Prime Number Distribution: Why 4k+3 Primes Lead the Race

The distribution of prime numbers reveals fascinating patterns that continue to surprise mathematicians. A particularly intriguing phenomenon emerges when we examine primes modulo 4, where primes of the form 4k+3 consistently maintain a lead over their 4k+1 counterparts, despite both categories being equally infinite in number.

The Sum of Two Squares Connection

Before diving into the distribution patterns, it's worth noting why this distinction matters. An odd prime p can be expressed as a sum of two squares if and only if p is of the form 4k+1. This elegant characterization connects number theory to geometry and has practical applications in cryptography. For instance, the prime 2255 − 19, which is used in cryptographic protocols like Curve25519 and Ed25519, belongs to this special category.

The Mersenne Prime Dominance

When examining record-breaking prime numbers, an interesting pattern emerges: all recent world records have been primes of the form 4k+3. This isn't coincidental but rather a consequence of how we discover large primes. Mersenne primes, which take the form 2^p − 1, are significantly easier to test for primality using the Lucas-Lehmer algorithm. This efficiency advantage means that the largest known primes have almost always been Mersenne primes since the algorithm's development in the late 19th century.

The Apparent Imbalance

At first glance, it might seem that primes congruent to 3 mod 4 outnumber those congruent to 1 mod 4. To investigate this, we can define a function f(n) that measures the ratio of these two categories among primes less than n:

f(n) = (# primes p < n with p ≡ 3 mod 4) / (# primes p < n with p ≡ 1 mod 4)

As n approaches infinity, this ratio converges to 1, confirming that both categories contain equally many primes in the infinite limit. However, the journey to this equality is far from straightforward.

The Lead Function and Chebyshev Bias

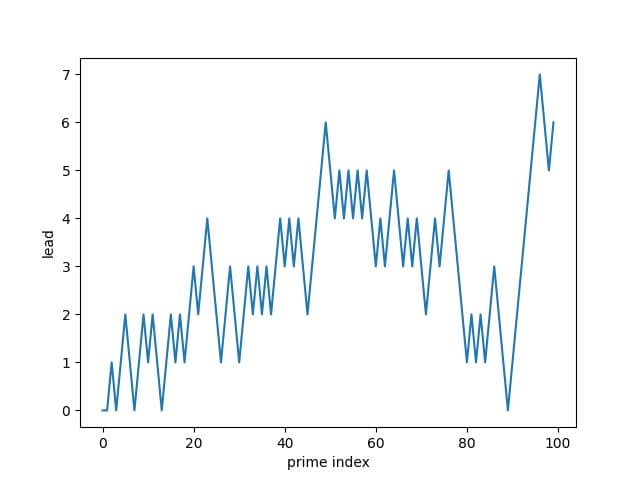
The more revealing perspective comes from examining the difference between the counts rather than their ratio. We can define a "lead function" g(n) that tracks how much the count of 3 mod 4 primes leads the count of 1 mod 4 primes:

g(n) = (# primes p < n with p ≡ 3 mod 4) − (# primes p < n with p ≡ 1 mod 4)

This function exhibits remarkable behavior. While f(n) > 1 if and only if g(n) > 0, the lead function g(n) does not converge as n approaches infinity. Instead, it oscillates between positive and negative values infinitely often, a phenomenon known as Chebyshev bias.

Visualizing the Oscillation

Using computational tools, we can track when the lead function changes sign by identifying the primes at which g(n) = 0. These transition points form a sequence (OEIS A038691) that reveals the irregular but persistent nature of the bias. The lead function is positive for long stretches, meaning 3 mod 4 primes maintain their advantage for extended periods, yet it crosses zero infinitely often, ensuring eventual equality.

The Mathematical Significance

This behavior exemplifies a broader principle in number theory: asymptotic equality doesn't preclude persistent local biases. The primes of the form 4k+3 maintain their lead not because they are more numerous in the infinite sense, but because of the intricate distribution patterns that govern prime numbers. This bias extends to other residue classes and relates to deeper questions about the distribution of primes in arithmetic progressions.

Practical Implications

The Chebyshev bias has implications beyond pure mathematics. In cryptography, the prevalence of 3 mod 4 primes among record holders affects which forms of primes are most practical for certain applications. Understanding these distribution patterns helps in algorithm design and in predicting the behavior of prime-related computations.

The race between 4k+1 and 4k+3 primes serves as a beautiful illustration of how number theory combines rigorous proof with surprising empirical phenomena, reminding us that even in the realm of pure mathematics, the journey to equality can be as interesting as the destination itself.