The Unifying Power of Linear Models: How Common Statistical Tests Are Just Special Cases

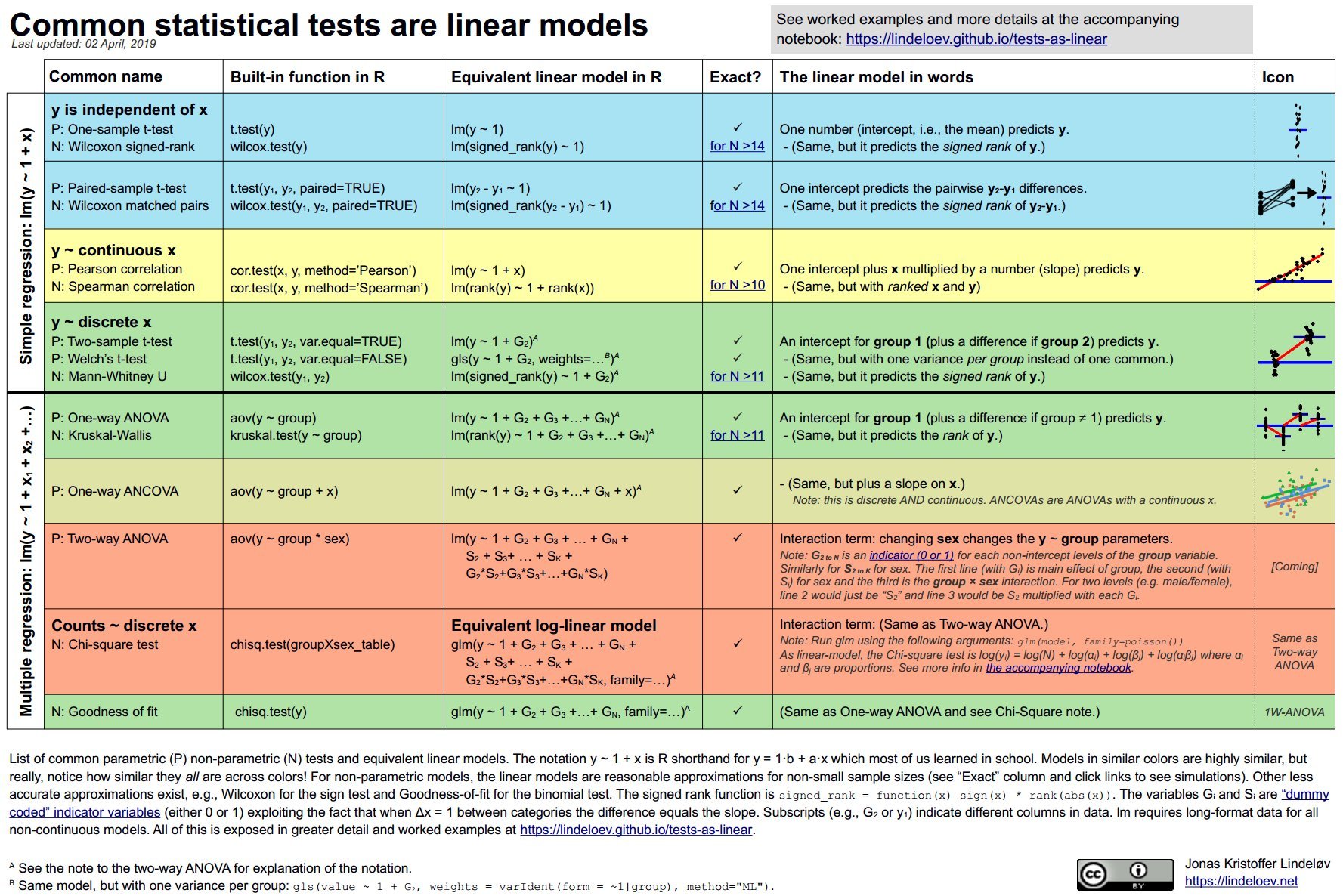
For decades, statistics education has treated t-tests, ANOVA, correlation, and non-parametric methods as distinct tools—each with separate assumptions and formulas. But what if these tests shared a common DNA? In a groundbreaking synthesis, data scientist Jonas Kristoffer Lindeløv demonstrates that most common statistical tests are special cases of linear models (y = β₀ + β₁x) or their rank-transformed cousins. This revelation collapses artificial boundaries in statistics education and empowers practitioners with a unified framework.

The Core Insight: Everything Is Regression

At the heart of this equivalence is a simple truth:

"Most common statistical models (t-test, correlation, ANOVA; chi-square, etc.) are special cases of linear models or a very close approximation. This beautiful simplicity means that there is less to learn."

Consider these equivalences:

1. T-tests become intercept models:

   • One-sample t-test: y = β₀ (test if β₀ = 0)
   • Independent t-test: y = β₀ + β₁*Group (test if β₁ = 0)

2. Pearson/Spearman correlation:

   • Pearson: y = β₀ + β₁x
   • Spearman: rank(y) = β₀ + β₁*rank(x)

3. ANOVA as multi-group regression:

   • One-way ANOVA: y = β₀ + β₁Group₁ + β₂Group₂ + ...

4. Non-parametric tests as rank transformations:

   • Wilcoxon signed-rank: signed_rank(y) = β₀
   • Mann-Whitney U: rank(y) = β₀ + β₁*Group

# R code showing t-test vs. lm equivalence
t.test(y)  
lm(y ~ 1)  # Same p-value & t-statistic

Why This Matters for Practitioners

• Reduced Cognitive Load: Instead of memorizing dozens of test assumptions, focus on linear model assumptions (independence, normality of residuals, homoscedasticity).
• Model Transparency: Coefficients (β) provide intuitive effect sizes—e.g., β₁ in an independent t-test is the mean difference between groups.
• Non-parametric Demystified: "Non-parametric" tests like Mann-Whitney U are simply linear models on rank-transformed data (accurate for N > 15).

The Teaching Revolution

Lindeløv argues that intro stats courses should start with linear models:

"Teaching linear models first and then name-dropping the special cases along the way makes for an excellent strategy, emphasizing understanding over rote learning."

This approach naturally extends to Bayesian and permutation-based inferences, avoiding early entanglement with p-values or type-I errors.

Beyond Basics: Chi-Square and ANCOVA

The framework scales elegantly:

• Chi-Square tests: Log-linear models (e.g., log(y) = β₀ + β₁*Group) handle contingency tables.
• ANCOVA: Simply add continuous covariates (e.g., y = β₀ + β₁Group + β₂age).

A Call for Change

The implications are profound: by embracing linear models as the "Swiss Army knife" of statistics, we can:

1. Unify parametric and non-parametric paradigms
2. Simplify software implementation (just lm() and rank transformations)
3. Focus on effect sizes and confidence intervals over ritualistic hypothesis testing

As Lindeløv concludes, this isn't just mathematical trivia—it's a lens that makes statistics more coherent, interpretable, and powerful. For developers and data scientists, it’s time to wield this unified toolset.

Source: Jonas Kristoffer Lindeløv's blog