The Mathematical Secrets Behind LLM Intelligence: Linear Representations and Superposition

As large language models grow increasingly sophisticated, researchers are uncovering surprising mathematical principles governing how these systems represent knowledge. Two fundamental concepts—linear representations and superposition—are providing new insights into the inner workings of AI systems.

The Geometry of Meaning

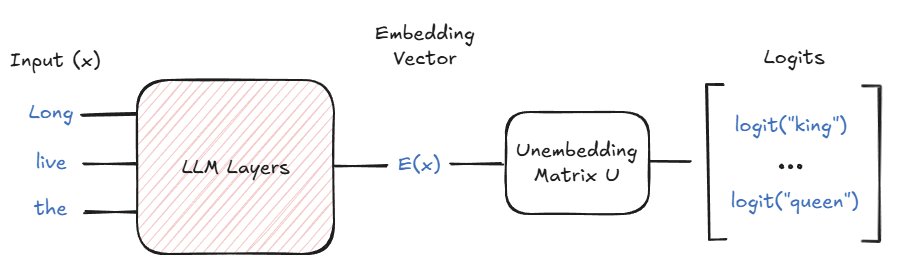
The linear representation hypothesis (LRH), first observed in early word embedding systems like Word2Vec, suggests that semantic relationships manifest as geometric relationships in vector space. The classic example shows that vector arithmetic captures semantic relationships: king - man + woman ≈ queen. This simple principle scales remarkably to modern LLMs.

Simplified LLM embedding/unembedding architecture (Park et al.)

Recent work by Park et al. formalizes this phenomenon across two spaces:

1. Embedding space: Where hidden states live, enabling interventions like E("Long live the queen") - E("Long live the king") = α·E_gender
2. Unembedding space: Where token probabilities are determined via relationships like U("queen") - U("king") = β·U_gender

Crucially, these representations are isomorphic—operations in one space mirror the other. Researchers validated this framework across diverse concepts (tense changes, language translation) in Llama-2, demonstrating consistent directional vectors for concept manipulation.

The Orthogonality Paradox

If concepts have linear representations, shouldn't unrelated concepts be orthogonal? Surprisingly, Euclidean orthogonality fails. Park et al. discovered that concept orthogonality only emerges under a causal inner product derived from the unembedding matrix itself.

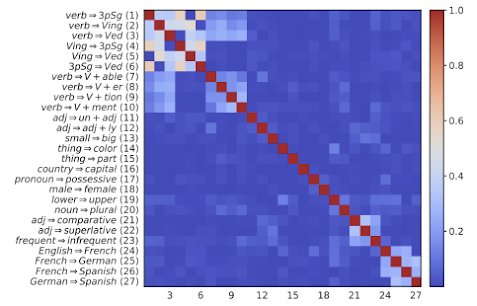
Concept orthogonality under causal inner product (Park et al.)

This raises a fundamental question: How do LLMs pack thousands of distinct features into relatively low-dimensional spaces (typically 2K-16K dimensions)? The answer lies in superposition.

Superposition: Beyond Intuition

Anthropic's research reveals that high-dimensional spaces enable exponentially many "almost-orthogonal" vectors through the Johnson-Lindenstrauss lemma. Unlike low-dimensional intuition suggests, interference between concepts becomes manageable through:

1. Nonlinear activation functions: ReLU gates enable constructive interference management
2. Feature sparsity: Rarely co-occurring features can safely superimpose
3. Regular geometric structures: Models naturally discover energy-minimizing configurations

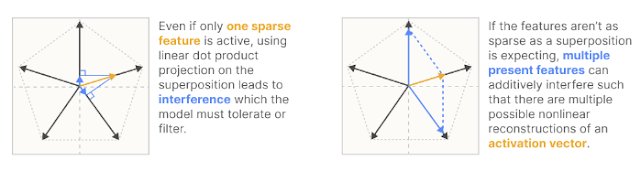
Interference patterns in superposition (Anthropic)

In synthetic experiments, embedding vectors spontaneously formed polyhedral structures like tetrahedrons and square antiprisms—identical to solutions for the Thomson problem of optimal spherical point distributions.

Square antiprism: Energy-minimizing 8-point configuration

Implications and Counterpoints

While this framework provides powerful interpretability tools, limitations exist:

• Scale sensitivity: Observed structures may not hold for billion-parameter models
• Nonlinear complexity: Attention mechanisms add layers of abstraction beyond embeddings
• Emergent behaviors: Higher-order interactions may not be linearly decomposable

As researcher Jeffrey Wang notes: "Features as linear representations, even if not the complete story, give us a window into how language complexity gets captured." The discovery of mathematical regularities in concept representation suggests that beneath the apparent complexity of LLMs lies an orderly geometric architecture—one where the counterintuitive properties of high-dimensional space enable remarkable compression of human knowledge.

This emerging understanding provides researchers with new levers for model steering and safety interventions. By mapping concept vectors, we gain targeted control over model behavior—from adjusting gender biases to modifying tense without retraining. As mechanistic interpretability advances, these mathematical foundations may prove as fundamental to AI engineering as Boolean logic is to computing.