Weak Factorization Systems: The Hidden Structure Uniting Category Theory and Topology

From Set Theory to Category Theory: The Factorization Journey

Every developer understands function composition, but category theory reveals deeper patterns. Consider a function (f: A \to B). As the source notes: "An average function between sets is neither surjective nor injective." Yet we can decompose it into 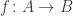a surjection followed by an injection using the image subset (X \subseteq B). This (Surj, Inj) factorization is unique – a property category theorists abstract into strict factorization systems.

"A (strict) factorization system specifies two classes of morphisms satisfying: each class is closed under composition and contains isomorphisms; every morphism factorizes; and the factorization is functorial."

Functoriality means factorization behaves predictably across commutative diagrams – a crucial property for algebraic consistency. But mathematics often demands flexibility. Enter weak factorization systems, where uniqueness gives way to lifting properties:

Weak factorization replaces strict functoriality with:
- ℒ = morphisms with left lifting property against ℛ
- ℛ = morphisms with right lifting property against ℒ

Topology's Surprising Constraints: Why Fibrations Surject and Cofibrations Inject

The real magic happens when we apply this framework to topological spaces. Through elegant proofs, the source establishes that:

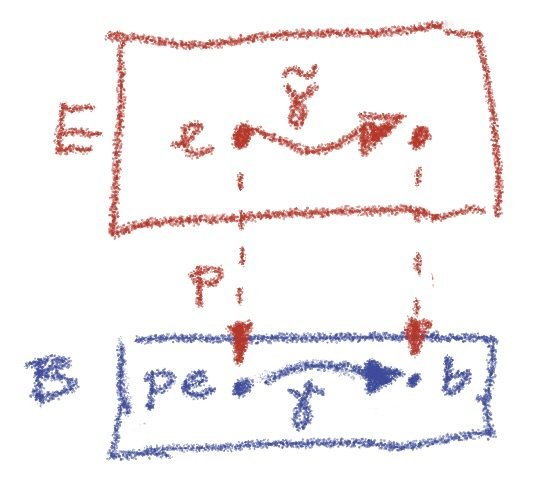
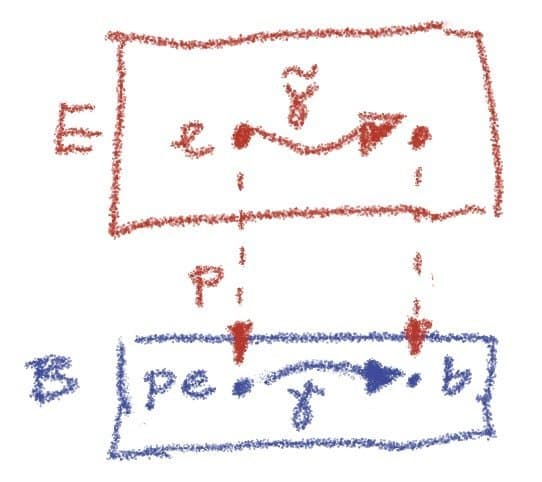
1. Fibrations are surjective (for non-empty, path-connected spaces):

   "If (p: E \to B) weren't surjective, a point (b \notin \text{im}(p)) couldn't have paths lifted from (B), violating the fibration's path-lifting property."

2. Cofibrations are injective: Proven via the ingenious mapping cylinder construction , which visualizes functions as "wires" connecting spaces. Non-injective maps would force premature point mergers, violating the homotopy extension property:

   *"The mapping cylinder (M_f) for (f: A \to B) is the quotient space ((A \times [0,1]) \sqcup B / (a,1) \sim f(a)). If (f) isn't injective, multiple wires merge at (B), breaking the cofibration's lifting condition under homotopy."

The (Cofib, Fib) Factorization: Topology's Answer to Category Theory

Just as sets admit (Inj, Surj) factorizations (using Axiom of Choice), topological spaces support weak (cofibration, fibration) factorizations. This forms a weak factorization system where:

• Cofibrations have left lifting against fibrations
• Fibrations have right lifting against cofibrations

This structure is foundational for Quillen model categories – the framework enabling modern homotopy theory. For developers working with type theory or formal verification, these concepts underpin homotopy type theory's treatment of equality as continuous deformation paths.

Why This Matters Beyond Abstraction

Understanding factorization systems isn't just mathematical elegance. They provide:

• Error handling paradigms: Decomposing complex operations into surjective/injective-like components
• Type system design principles: Inspiring approaches to canonical embeddings and projections
• Concurrency models: Analogies to path lifting in distributed system state synchronization

As we push boundaries in quantum computing and homotopy-inspired type systems, these categorical patterns become increasingly vital. The marriage of topological intuition and algebraic rigor continues to shape how we construct robust computational abstractions.

Source: Weak Factorization Systems by Bartosz Milewski